Appendix 2: Using Dice¶
You can (and should) generate seed phrases with dice.
This is because true randomness is surprisingly difficult to achieve on a computer. This is referred to as entropy, that is, a measure of randomness.
For example, a fair coin flip is 1-bit of entropy; flipping two coins can offer 2-bits of entropy (4 possible outcomes). But if one of the coins is unfair and always lands on heads, then we're back to only 1-bit of entropy from the first coin.
The goal of a seed phrase is to achieve the maximimum amount of entropy that would prevent anyone from deriving or guessing your seed phrase.
Beware of Low Entropy
A 24-word seed phrase is nothing more than an encoding of a 256-bit number (with a checksum at the end). If all 256-bits were the same, that is, all zeros except the checksum, then this would have very low entropy.
The seed phrase would simply be,
abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon abandon art
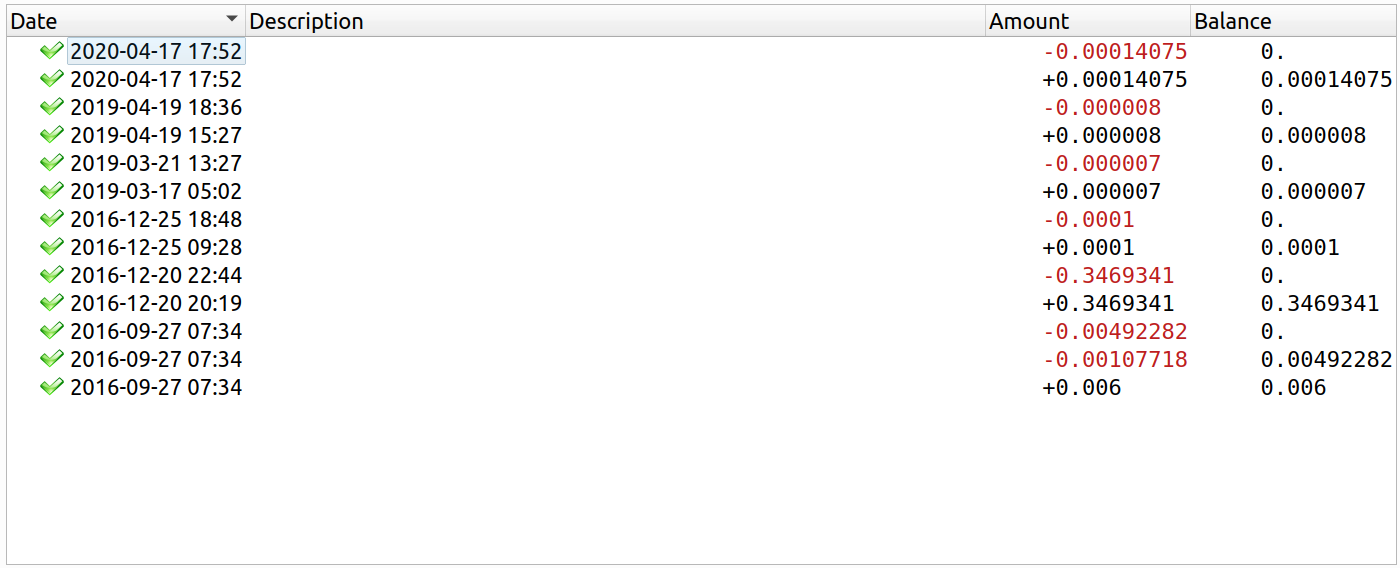
That's 23 abandon's and 1 art
Turns out this ridiculous 1-bit of entropy phrase was actually used before. You can recover this wallet and view the transaction history for yourself. For 2-hours in 2016 there was 0.3469341 Bitcoin stored with this key. Perhaps these transactions are part of a Steganographic puzzle, and this is the first entry into finding a hidden fortune. Or perhaps someone lost their Bitcoin because of low entropy.
How to get High Entropy?
In the above example, it took less than a second to discover a seed phrase protected only by 1-bit of entropy.
How long would it take for 256-bits of entropy?
256-bits of entropy is difficult to fathom. You might hear "centuries" or "millions of years", but it's more like, "beyond the age of the universe even with planet-sized super-computers powered by Dyson-spheres around every star."
It's the same as flipping a coin 256 times. Not exactly a difficult task, but assuming it was a fair coin then this would get you 256-bits of entropy, and the odds of anyone guessing or deriving that exact 256-bit number is impossible (unless they watched you flipping the coin).
It's like finding a needle in a haystack -- if the haystack was the entire universe, and also the needle was invisible.
Numeric Base of Dice¶
We usually deal with Base-10 (decimal) and Base-2 (binary). In fact, when we say "bits" we're referring to the length of a binary number.
But we can represent a number in any arbitrary base. And this is important because one of the best sources of true random numbers is fair dice rolls.
A common 6-sided dice can be used to generate a 256-bit number, but doing so can be somewhat confusing. You may try to map the numbers to binary but you'll find it's not so easy (1 dice gives you 2.5-bits of entropy). To be safe you could just map odd and even rolls to binary 1 and 0, but this requires 256 dice rolls and isn't very efficient.
A better aproach is to use a Base-6 representation of a 256-bit number, which would require 100 dice rolls. This is the number of fair dice rolls necessary to achieve 256-bits of entropy.
Alternatively, and my recommendation, is to use an 8-sided dice, the kind commonly found in role-playing games. A fair 8-sided dice roll has exactly 3-bits of entropy (meaning every 8-sided dice roll gives you exactly 3 of the desired 256-bits). With this approach you'll need 86 rolls to generate sufficient entropy for a seed phrase.
256-bits in other Bases¶
| Numeric Base | length | Description |
|---|---|---|
| Base-2 (binary) | 256 | coin tosses |
| Base-6 | 100 | dice rolls |
| Base-8 (octal) | 86 | 8-sided dice rolls |
| Base-10 (decimal) | 78 | 780-Quattuorvigintillion |
| Base-20 | 60 | 20-sided dice rolls |
| Base-64 | 43 | I-Ching Hexagrams |
| Base-2048 | 24 | seed words |
How to Ensure Fair Dice¶
There's a strange phenomenon in the Bitcoin community where they insist on casino-grade dice; as if "casino" is an infallible authority on dice grading that we should trust our life savings with.
Don't trust, verify
If you're concerned with the fairness of dice, then you should verify your dice with a saltwater balance test. Whether using "AAA casino-grade razor-edge precision dice" or using the dice you got from a board game, a saltwater test can verify if the dice is balanced or not.
Just saying "Casino-grade" is not a verification.
In most cases, even a slightly unbalanced dice will still roll fairly, but it's recommended to verify that a given set of dice (casino-grade or otherwise) is balanced so you'll know it can generate the desired level of entropy.
Saltwater Balance Test¶
You'll find many examples online, mostly from dedicated communities around board games, RPGs, and gambling aficionados. God bless our fellow nerds.
In practice, you simply need a cup of supersaturated saltwater. This just means the water cannot absorb any more salt and that your dice will become buoyant.
- In a clean cup, fill with clean filtered water
- Add salt, a lot of salt, and stir till the salt is fully absorbed in the water
- Keep adding salt and stirring until your dice becomes buoyant
Once the dice is floating towards the surface you'll be able to test if it's balanced or not. Simply push the dice with a pencil or chopstick.
An unbalanced dice will float upward favoring one side. It will be obvious. In practice this could be due to air-bubbles or inconsistent materials.
Using this very simply technique you can verify your dice are balanced and can safely be used to generate high levels of entropy. You'll find the "casino-grade" dice offer no benefit over standard board game dice, and most importantly you'll have verified your dice.
No trust required!
Dice and Paper¶
To really understand the security and ownership of your private keys, you ought to generate seed phrases by hand, with dice and paper. You will need to transfer the seed phrase to a secure airgapped computer and generate a checksum, however everything before that can be done by hand.
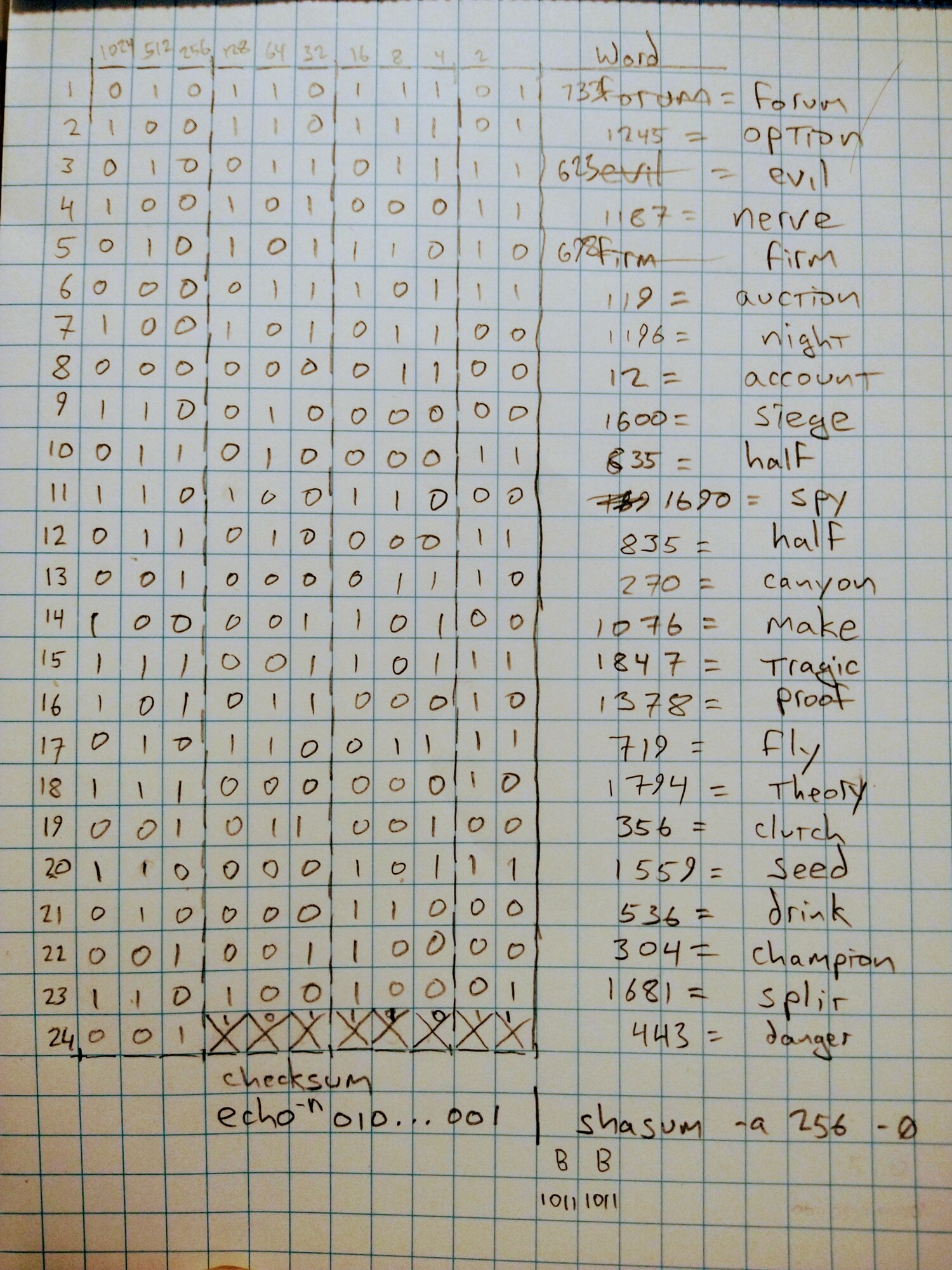
I recommend using 8-sided dice that have been verified through a saltwater balance test. This will make the mapping much easier because an 8-sided dice corresponds exactly to 3-bits of entropy. Use the following chart to map each number to its binary equivalient.
| 8D dice roll | 3-bits |
|---|---|
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 000 |
Each number on the dice corresponds directly to its binary representation, except 8, which in binary is "1000" and so this is just the lower 3-bits of 8 in binary. Because an 8-sided dice maps perfectly into 3-bits, it is very easy to roll and record the entropy bits directly in binary.

Write Dice Rolls in Binary¶
Each word in the seed phrase is exactly 11-bits (2048 possibilities).
And each dice roll will provide 3-bits.
You'll want to keep rolling until you fill out all but the last 11-bit word, and 3-bits of the 24th word. As you fill out 3-bits at a time, you can go left-to-right and top-down, and stop after writing 3-bits into the 24th word. The remaining 8-bits of the final word are calculated through a checksum which we'll discuss next.
What about 12-Word Seeds?
You could also do 12-word seeds, which will give you 128-bits of entropy.
You'll fill out 11 of the 11-bit words and 7-bits of the 12th word. The remaining 4-bits will be the checksum.
In either case, you'll need to compute the checksum to arrive at a valid final word. This simple checksum is to ensure that you've got a valid seed phrase.
A common approach is to add an additional passphrase to the seed words, like a 13th or 25th word, but not constrained to the BIP-39 word list. This passphrase can provide additional bits of entropy, and using a strong passphrase can easily add enough entropy to make a 12-word plus passphrase seed as strong as a 24-word seed.
Complete the Checksum¶
Completing the final word requires a checksum.
In this
case a sha256sum
of the 256-bits of entropy.
Remember the 24th word has 8-bits for
the checksum, which should be the
first 8-bits of the shasum.
This may sound complicated, but you can use the same secure airgapped computer you plan on using to sign transactions and Self Custody your Bitcoin. If you're just testing this approach feel free to use any computer to calculate the checksum bits.
You will run the following shell command, and
you'll need to type your exact binary number.
For brevity, I will use 010...001 to represent the full
256-bit binary number seen in the worksheet above.
$ echo 010...001 | shasum -a 256 -0
bbcb5d63c87ee0b833f656ae55db8e4ba0f0d4f8cab91be038b5c32de106696a
$
To compute the same using python is a little more involved, but helpful if you want to verify.
python sha256sum
>>> import hashlib
>>> import binascii
>>>
>>> bin_str = '0101101110110011011101010011011111001010001101010111010000011101111001010110000000001100110010000000110100001111010011000011010000110010000111010000110100111001101111010110001001011001111111000000100010110010011000010111010000110000010011000011010010001001'
>>> entropy_hex = format(int(bin_str, 2), '064x')
>>> hex_bytes = binascii.a2b_hex(entropy_hex)
>>> hashlib.sha256(hex_bytes).hexdigest()
'bbcb5d63c87ee0b833f656ae55db8e4ba0f0d4f8cab91be038b5c32de106696a'
>>>
The shasum is a Base-16 (hexidecimal) number, representing the 256-bit shasum of the entropy bits we got from the dice rolls.
bbcb5d63c87ee0b833f656ae55db8e4ba0f0d4f8cab91be038b5c32de106696a
To get the checksum needed for our 24th word,
take the first two hexidecimal digits of the shasum,
in this case bb,
and convert to binary.
Each hexidecimal digit is exactly 4-bits,
and b is 1011,
so bb is 10111011
If you are not sure how to convert hexidecimal digits to binary, or you want to verify you did it correctly, you can verify in python,
>>> format(int("bb", 16), "08b")
'10111011'
>>>
Once you have the first 8 binary digits of the shasum, simply add those 8-bits to the worksheet to complete your 24th word. The 3-bits from dice plus the 8-bits from the shasum will complete all 11-bits of the final word.
Seed Word Lookup¶
Now that you have all the binary values, you can resolve each of the 24 values to its corresponding BIP-39 seed word.
There are many ways to do this, and a helpful place to start is to reference a printable version of the BIP-39 words. There are many examples online, and I have included one here,
0 00000000000 abandon
1 00000000001 ability
2 00000000010 able
...
2045 11111111101 zero
2046 11111111110 zone
2047 11111111111 zoo
In practice, I find trying to match the binary extremely difficult. And instead I opted to convert each of the 11-bit numbers to decimal. You can do this fairly quickly if you're good at adding numbers that are all powers of 2 (e.g., 512 + 64 + 8 = 584).
If you're like me you can use an old pocket calculator, or even better, use the secure airgapped computer that you plan to use for Self Custody.
Python makes a wonderful calculator,
>>> int('01011011101', 2)
733
>>>
You can then reference the official BIP-39 words and see that 733 corresponds to "forum"
Seed words start at 0
Be careful to avoid fencepost errors as the line-numbers start at 1 but the seed words start at 0
Alternatively, you can do this in python very easily if you already have the official BIP-39 words on your airgapped computer, e.g.,
>>> with open('english.txt') as f:
... seed_words = f.read().splitlines()
>>>
>>> seed_words[733]
'forum'
>>> seed_words[1245]
'option'
>>>
This almost feels like cheating, but it's a nice reminder to include the BIP-39 word list on your secure airgapped computer. However you do it, manually or using the airgapped computer, you should now have all 24 words of your seed phrase.
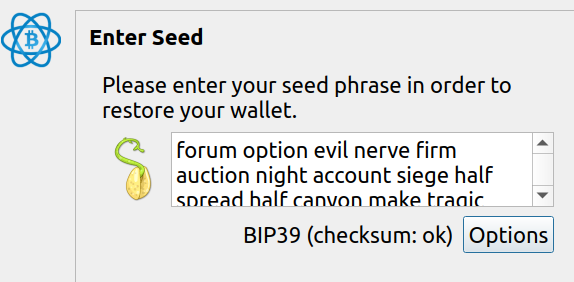
forum option evil nerve firm auction night account siege half spread half canyon make tragic proof fly theory clutch seed drink champion split danger
Verify Seed Phrase¶
Now that you have all 24 words, you can use them in the wallet software of your choice. If you made a mistake anywhere the checksum will very likely fail.
I was able to verify this seed phrase in electrum --
electrum
And I can view the master public key (go to "wallet" -> "information" in electrum) --
electrum
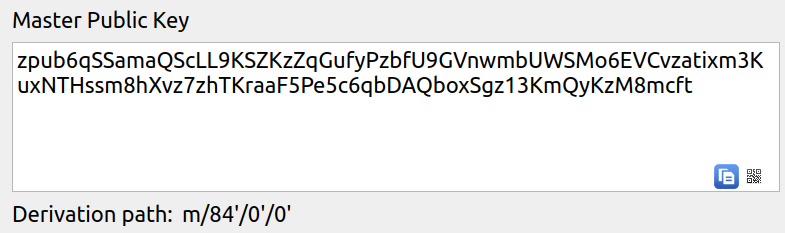
Additionally, I was able to verify the seed phrase and the entropy bits using the Mnemonic Code Converter --
And that's it!
What started with dice and paper is now a valid and secure Bitcoin private key.
Dice and Computer¶
We can use our airgapped computer to convert dice rolls into a seed phrase. This will give us the verified entropy of dice rolls, and when done correctly can be more secure than dice and paper.
This technique is also applicable to other methods of creating 256-bits of entropy, from I-Ching Hexagrams to Tarot cards. All that is required is a list of unique characters to represent the set.
dice-rolls to number
1 2 3 4 5 6 7 | |
number to dice-rolls
1 2 3 4 5 6 | |
If you already have the official BIP-39 words on your airgapped computer, e.g.,
>>> with open('english.txt') as f:
... seed_words = f.read().splitlines()
>>>
>>> seed_words[0]
'abandon'
>>> seed_words[2047]
'zoo'
>>>
Roll the dice and record them into a variable, e.g., d6_rolls
>>>
>>> d6_rolls = '1325251343253343214251563241321214344521641246163226332132423346231453554151345112124463226413335644'
>>>
Next you'll want to verify the length,
>>> len(d6_rolls)
100
>>>
Let's convert this to a number,
>>>
>>> entropy_number = dice2n(d6_rolls, '123456')
>>> entropy_number
41477543854087285771122632882271155796101921343012082862722996391061926720649
>>>
You've got the number, now we format it as a binary string,
>>>
>>> entropy_bin = format(entropy_number, '0256b')
>>> entropy_bin
'0101101110110011011101010011011111001010001101010111010000011101111001010110000000001100110010000000110100001111010011000011010000110010000111010000110100111001101111010110001001011001111111000000100010110010011000010111010000110000010011000011010010001001'
>>>
Compute the checksum
>>>
>>> import hashlib
>>> import binascii
>>>
>>> entropy_hex = format(entropy_number, '064x')
>>> hex_bytes = binascii.a2b_hex(entropy_hex)
>>> entropy_sha = hashlib.sha256(hex_bytes).hexdigest()
>>> entropy_sha
'bbcb5d63c87ee0b833f656ae55db8e4ba0f0d4f8cab91be038b5c32de106696a'
>>>
Add first 8-bits of the checksum, to produce the 264-bit string (that is, 24 words, each with 11-bits)
>>>
>>> seed_bin = entropy_bin + format(int(entropy_sha[0:2], 16), '08b')
>>> len(seed_bin)
264
You can now lookup seed words using 11-bit slices,
>>>
>>> seed_words[ int(seed_bin[0:11], 2) ]
'forum'
>>>
Using the above approach, you can loop through all slices,
>>>
>>> [seed_words[int(seed_bin[x:x+11],2)] for x in range(0,264,11)]
['forum', 'option', 'evil', 'nerve', 'firm', 'auction', 'night', 'account', 'siege', 'half', 'spread', 'half', 'canyon', 'make', 'tragic', 'proof', 'fly', 'theory', 'clutch', 'seed', 'drink', 'champion', 'split', 'danger']
>>>
dice to seed phrase
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
You can use the above to generate a seed phrase from your dice roll string,
>>>
>>> my_seed_phrase = dice_to_seed_phrase(d6_rolls, '123456', seed_words)
>>> for w in my_seed_phrase:
... print(w)
...
forum
option
evil
nerve
firm
auction
night
account
siege
half
spread
half
canyon
make
tragic
proof
fly
theory
clutch
seed
drink
champion
split
danger
>>>
dice prompt mini app
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | |
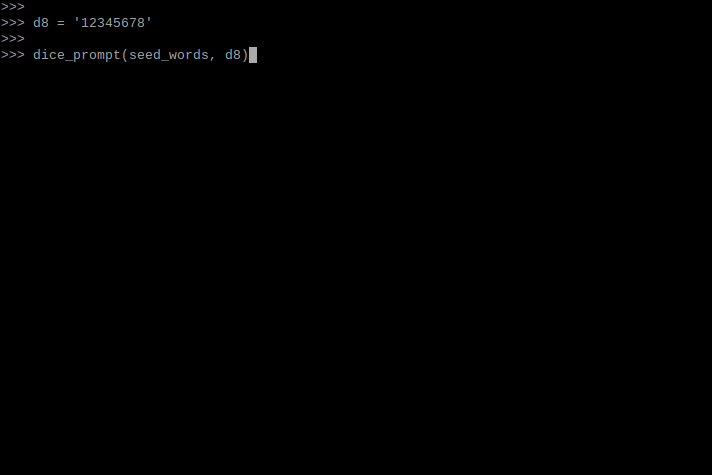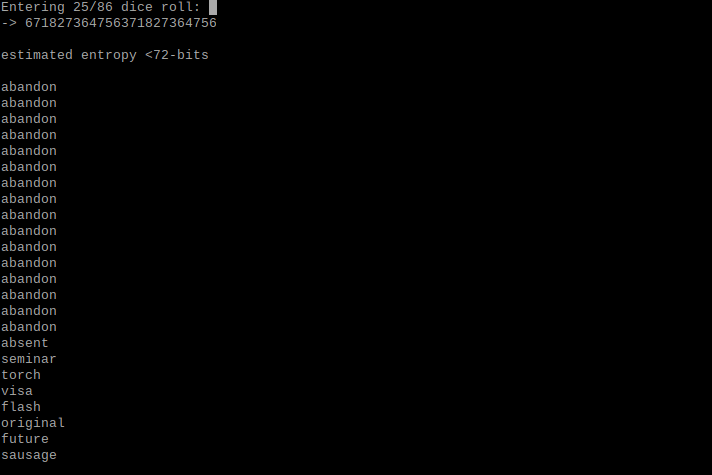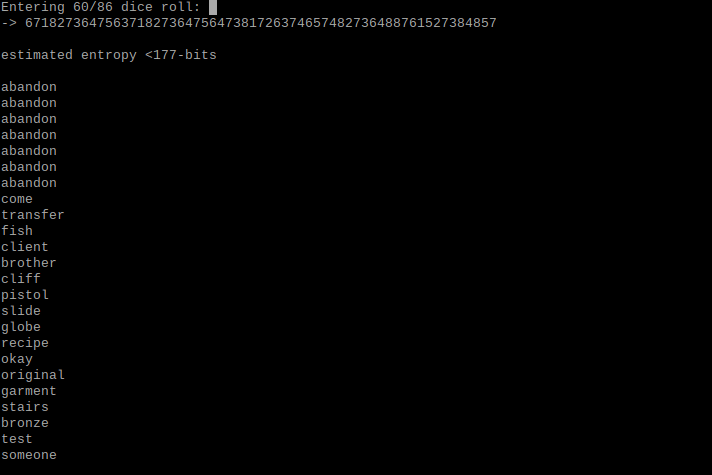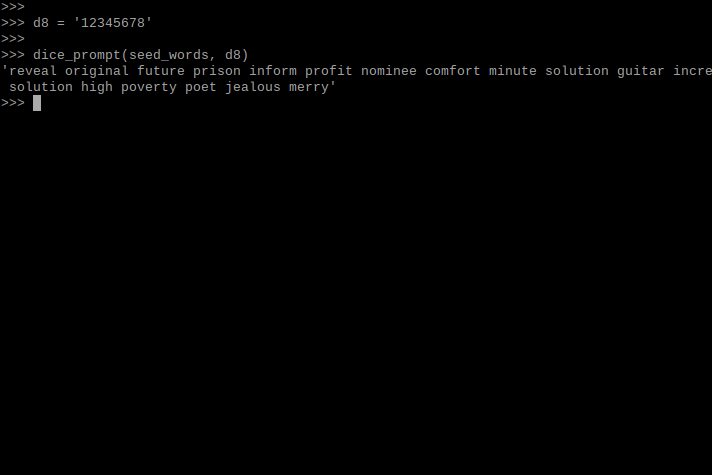
The above code can be found here, in a simplified app (under 100-lines). This can be run on even the most basic hardware (such as an airgapped computer).